机器学习基本概念

输入一个东西输出一个数字的任务就称为回归分析（Regression）

第一步：找到一个未知的函数式，已知大量变化的 x 和大量结果 y ，这个过程成为学习（Learning）或训练（Training）
步骤 1：我要找一个什么样的函数
步骤 2：我有哪些选择（第一步、第二部没有先后关系）
步骤 3：选一个最好的
第二部：定义一个 Loss from Training Data：用来评估函数好坏的参数，是自己定义的一个函数。可以是计算结果平均差值（MAE），可以是平均平方差值（MSE）。

最佳化：Gradient Descent
- 学习比率：learning rate
- 局部最优解、全局最优解、

第三步：Optimization：找一组参数，让某一个目标函数的损失函数 Loss 达到最大或最小，这种事情叫做 Optimization

定义一个函数式

Linear models（线性模型）： $y=b + wx_1$

Piecewise Linear Curves（分段线性曲线）：可以用 sigmoid 函数表示如下：

y = c\frac{1}{1 + e^{-(b+wx_1)}} = c*sigmoid(b+wx_1)

不同的改变，会有不同的效果

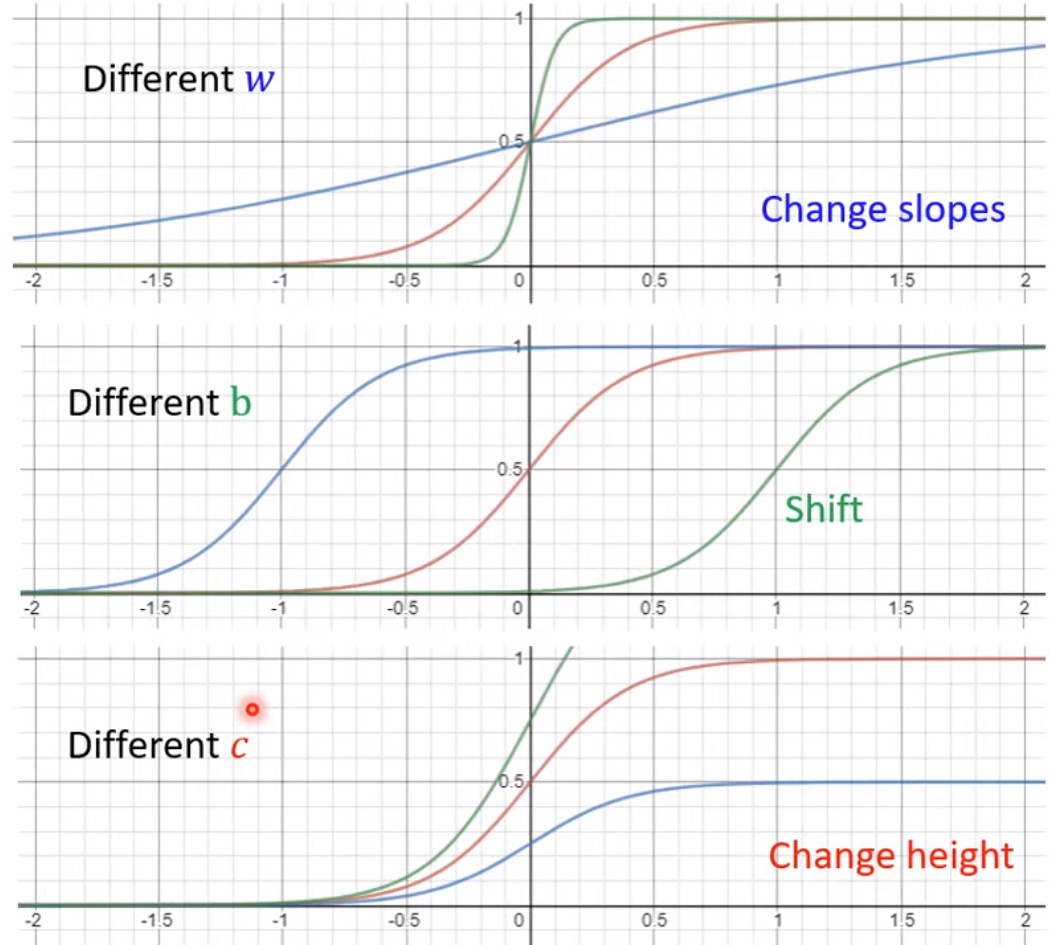
image.png|650

得到分段线性曲线公式

image.png|650

同步转化：

image.png|650

Sigmoid->ReLU
ReLU：Rectified Linear Unit： $c\; max(0,b+wx_1)$

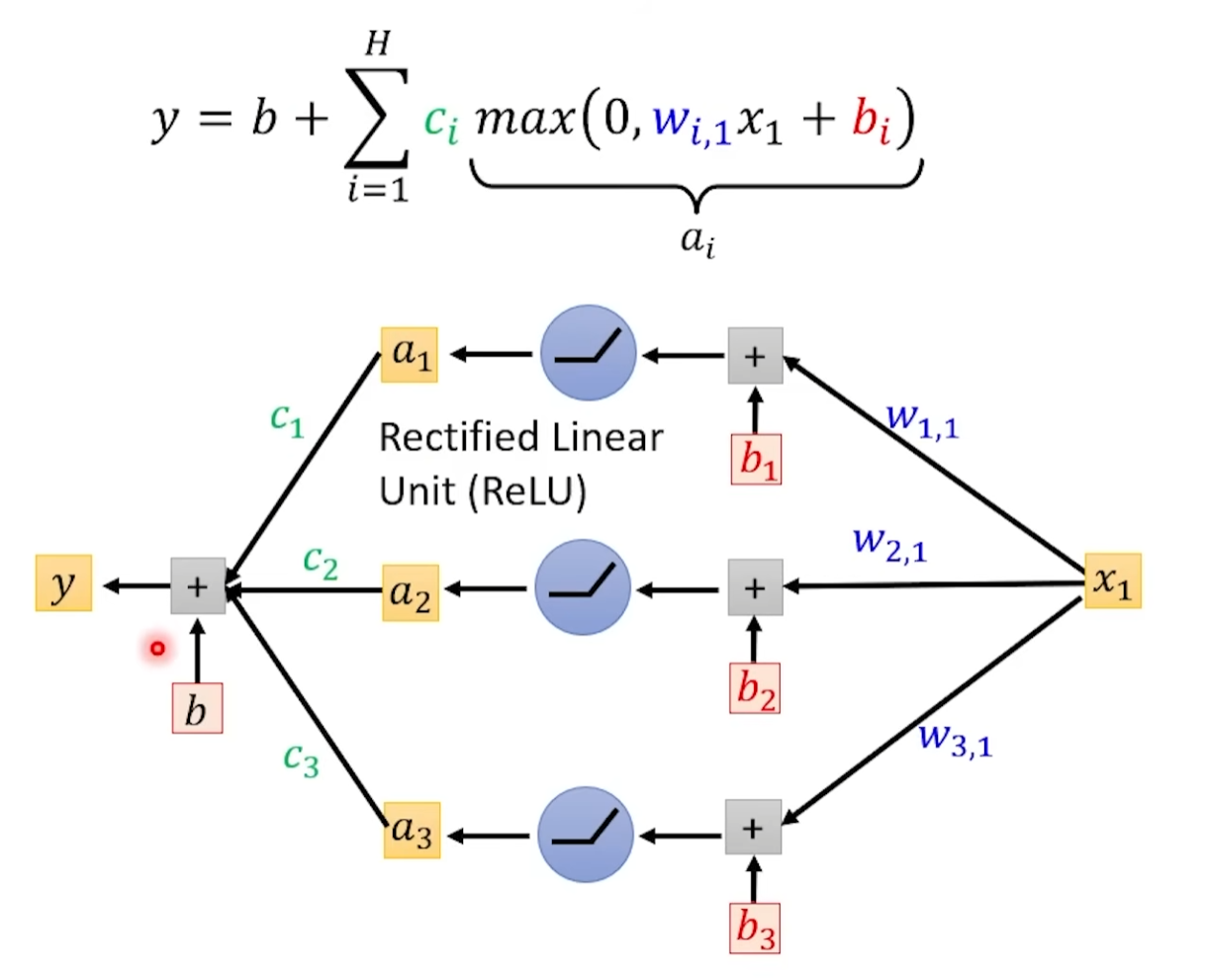
image.png|550

上面是一个参数得到的结果，如果我们有多个如下是示意图

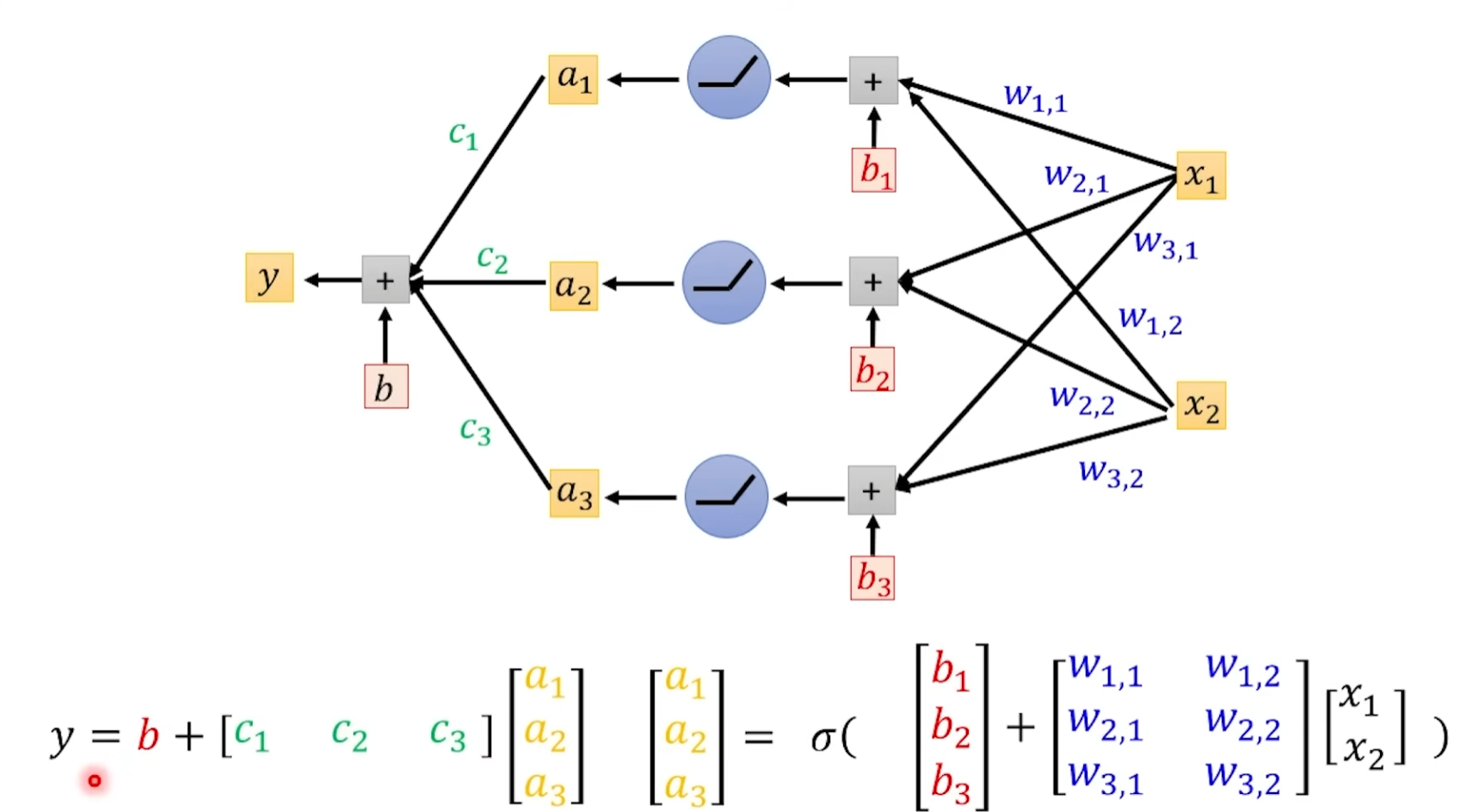
image.png|550

然后我们将结果 a1、a2、a3 再进行一次

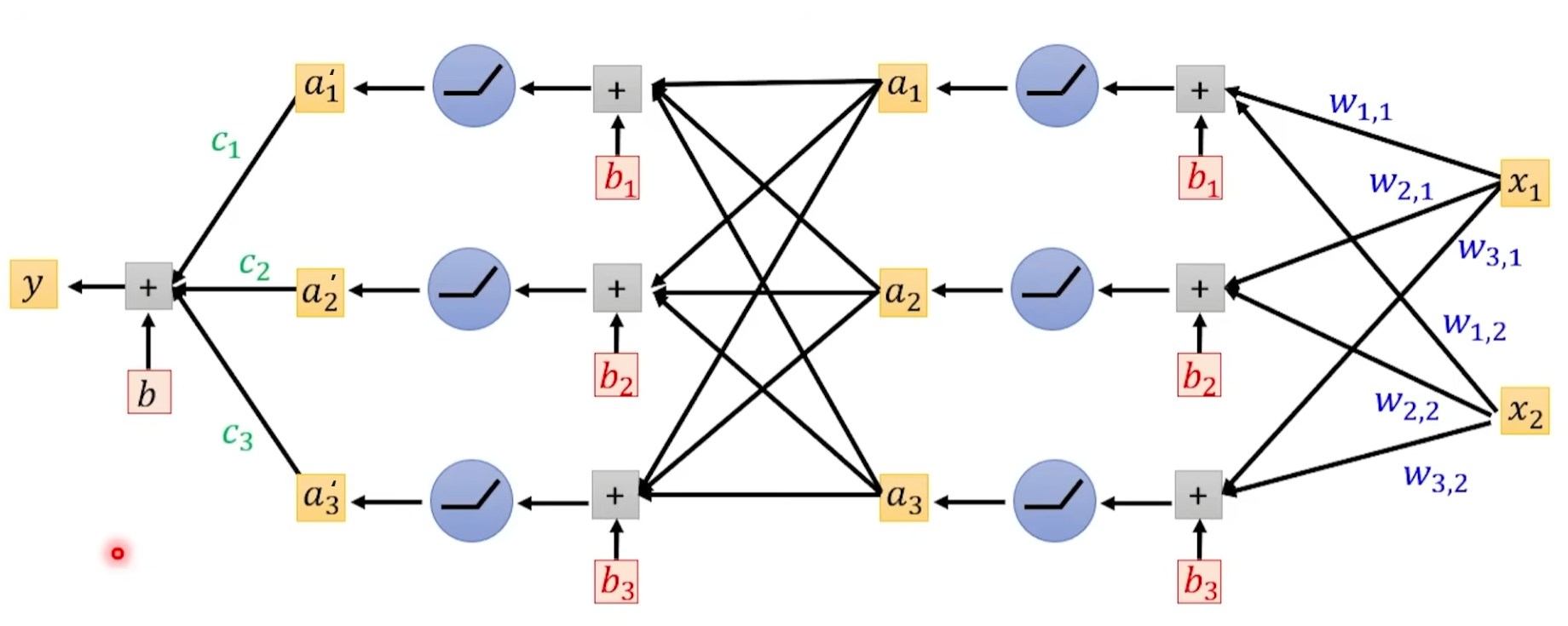
image.png|550

我们将 ReLU 和前面的乘积加 b 整体称为一个神经元（Neuron），多个 Neuron 就是 Neural Network（类神经网络）

我们将一次所有的神经元计算成为一个 Layer，有时候前面会加 Hidden 区分输入，输入的 Layer 叫 Input Layer 其他叫 Hidden Layer
很多 hidden layer 就是 Deep。最终就是 Deep Learning

这个公式有一个统称叫 Activation function

反向传播 backpropagation

Loss from Training Data

定义一个 Loss 的计算方法，把 Loss 的函数方程写出来，这里用平均方差的方式计算 Loss

就是测试预测的结果减去实际结果求平方，将所有的平方后的结果求和再平均就是均方差，这个值越小说明结果约接近。

数学式：

L = \frac{1}{N} \sum_{i=1}^{N} (y^i - \hat{y}^i)^2

Optimization

让某一个目标函数的损失函数（Loss）达到最大或最小，即逐渐让 Loss 变化的方法，这种事情叫做 Optimization

Gradient Descent (梯度下降法)

梯度下降发是常用的 Optimization，分为基础梯度下降、等

基础梯度下降（Vanilla Gradient Descent）

通常用的就是基础的梯度下降方法，英文作：Vanilla Gradient Descent
Vanilla 原意香草，放在 Gradient Descent 表示这是一个简单的、原味的方法。

从简单往复杂理解下方法，先带入一个简单的线性函数（假如这个函数就是目标函数）： $y = wx + b$ ，其中假设 w、b 就是函数的参数，x 是输入的变量。

将 $y = wx + b$ 带入 $L = \frac{1}{N} \sum_{i=1}^{N} (y^i - \hat{y}^i)^2$ 得到：

L(w,b) = \frac{1}{N} \sum_{i=1}^{N} (wx^i + b - \hat{y}^i)^2

此时训练函数时，程序需要考虑 2 个参数的变化，w、b，所有 w 记作 w* ，所有 b 记作 b*，可以将得到最好的 Loss 记作 $w*,b* = arg\min\limits_{w,b}L(w,b)$

2 个参数我们可以画出 w、b、loss 之间的图形，效果如下

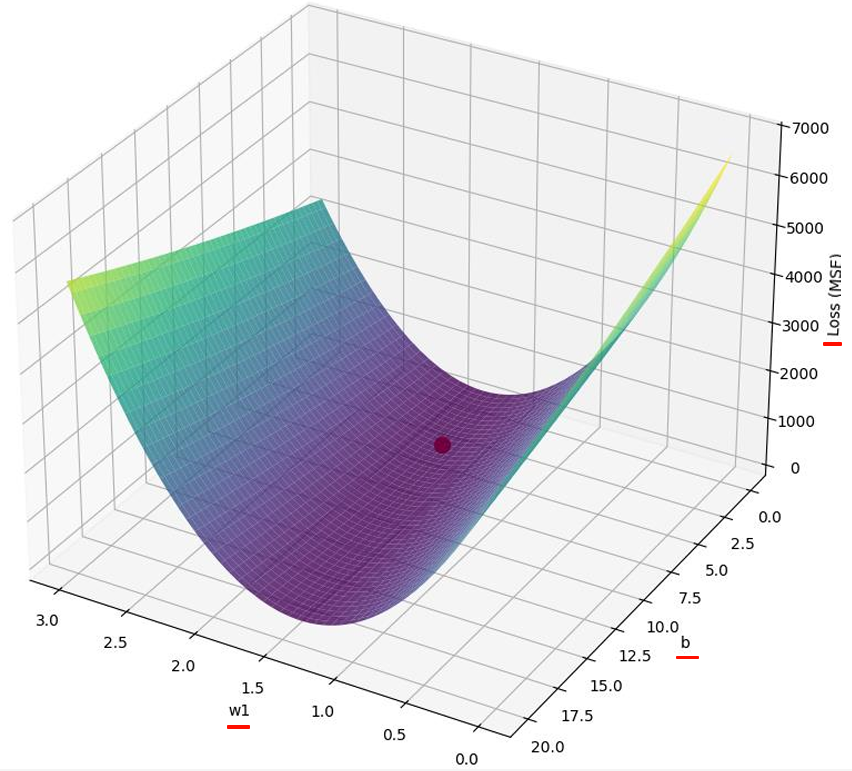
image.png|550

我们可以很直观的看到哪里是最优的 Loss，但如果参数再多，是无法画出图形，当初始化随机选择参数后，我们需要一个方法来给程序提供调整参数变化的依据。这时我们引出梯度下降。

如果要反应某个参数对入参 x 得到结果 y 的影响大不大，首先能想到偏导数。

偏导数（英语：partial derivative）的定义是：一个多变量的函数（或称多元函数），对其中一个变量（导数）微分，而保持其他变量恒定。
一个多元函数因为曲面上的每一点都有无穷多条切线，描述这种函数的导数相当困难。==偏导数就是选择其中一条切线，并求出它的斜率==。
函数 $\displaystyle f$ 关于变量 $\displaystyle x$ 的偏导数写为 $f_x'$ 或 $\frac{\partial f}{\partial x}$ 读作：f 对 x 的偏导数
偏导符号 $\partial$ 是全导符号 $\mathrm{d}$ 的变体

还是 $y = wx + b$ 这个函数的 Loss 函数 L，其中 x 、 $\hat{y}^i$ 是输入，在训练时这两个值是已知的。而 w、b 是它的参数，是要求解的。那么对这个函数而言就是一个多元函数
如果我们只考虑 w 这个参数的变化，那么 L 对 w 的偏导数就是 $\frac{\partial L}{\partial w}$ ，在训练时，w、b 的值是随机给的，则在在指定的初始 w、b 这一点上时 L 对 w 的斜率就可以计算，可以通过这个斜率知道 w 向那一侧移动能让 Loss 更优，这里目的是 Loss 越小越好，则 w 向哪一侧移动能让 Loss 变小

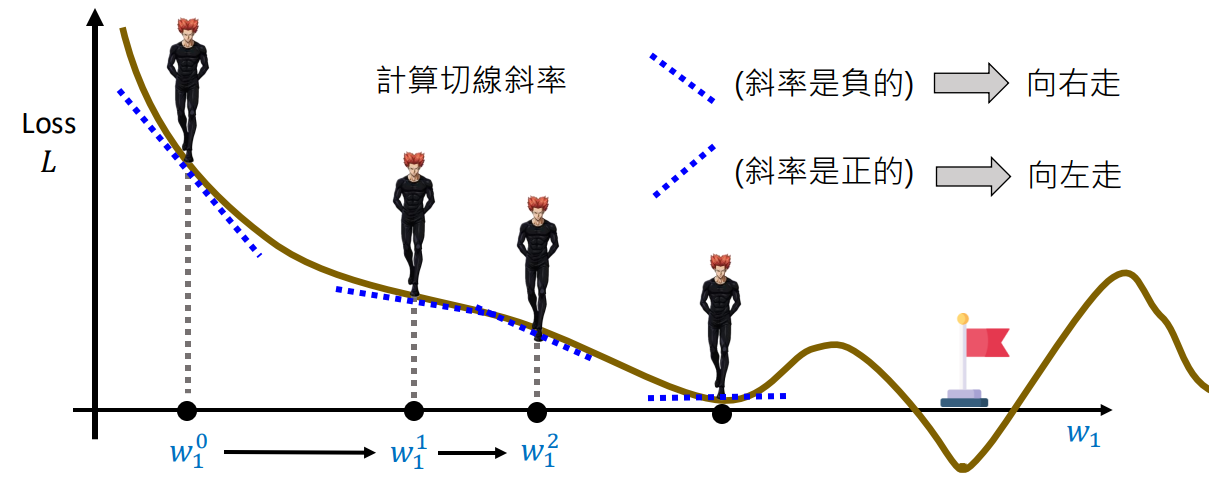
image.png|550

知道了移动方向，还需要知道每次移动多少，跟斜率关联如果斜率越大移动越多。
为了方便改变移动距离，我们引入一个变量（ $\eta$ 读作伊塔 (yī tǎ) 或艾塔 (ài tǎ)）控制让斜率乘以上这个变量作为移动距离，就能够达到斜率越大移动越大，斜率越小移动越小，我们还能宏观调节移动距离（斜率的倍数）
即：

w^1 = w^0 - \eta \frac{\partial L}{\partial w}\mid _{w=w^0,b=b^0}

同理 b 参数得到下一次改变的值为：

b^1 = b^0 - \eta \frac{\partial L}{\partial b}\mid _{w=w^0,b=b^0}

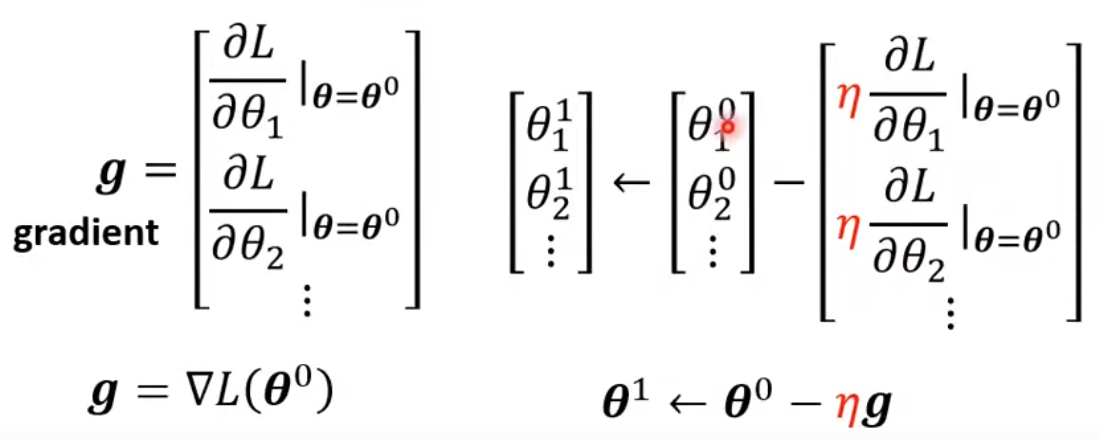
推至再多参数，将 w、b... 用一个向量 $\theta$ 代替

\theta = \begin{bmatrix} \theta_1 \\ \theta_2 \\ \vdots \end{bmatrix}

向量中每个元素都在 $\theta^0$ 时求 L 对该元素的偏导得到向量 $g^0$ ，其中这个 g 称之为 gradient

g^0 = \begin{bmatrix} \frac{\partial L}{\partial \theta_1}\mid _{\theta=\theta^0} \\ \frac{\partial L}{\partial \theta_2}\mid _{\theta=\theta^0} \\ \vdots \end{bmatrix}

通过这个 $g^0$ 能计算出新的 $\theta^1$

\theta^1 = \begin{bmatrix} \theta_1^1 \\ \theta_2^1 \\ \vdots \end{bmatrix} = \begin{bmatrix} \theta_1^0 \\ \theta_2^0 \\ \vdots \end{bmatrix} - \eta \begin{bmatrix} \frac{\partial L}{\partial \theta_1}\mid _{\theta=\theta^0} \\ \frac{\partial L}{\partial \theta_2}\mid _{\theta=\theta^0} \\ \vdots \end{bmatrix}

总结，通过这个计算就能到的新的参数，通过新的参数再次执行新的函数得到新的 Loss ，循环往复知道 Loss 结果达到满意，保存参数。

image.png|650

把所有的数据 L 分成多个 Batch，每组 Batch 生成一个 gradient，所有的 Batch 都 update 一次称为一个 epoch（纪元、时代）

反向传播（backpropagation） 一个比较有效的算法但也是 Gradient Descent。Chain Rule

识别需要更好的 Optimization 还是更换 Generalization

泛化（generalization）: 是机器学习中的一个核心概念，指的是模型在训练数据之外的新数据上表现得如何。换句话说，泛化能力衡量的是模型能否在未见过的样本上做出正确的预测或推断。
过拟合（Overfitting）: 当模型在训练数据上表现得非常好，甚至可以完全记住训练数据中的每个细节，但在新数据上表现很差时，就发生了过拟合。过拟合的模型过于复杂，以至于学习到了训练数据中的噪声和异常模式。这种情况下，模型的泛化能力非常差。例子：可以把过拟合比作一个学生考试时背诵了所有题目的答案，但当考试内容稍微变化时，学生却无法灵活应对。模型就像这个学生，只记住了训练数据的细节，而不是学习到数据背后的通用模式。
欠拟合（Underfitting）：欠拟合是模型过于简单，无法很好地捕捉训练数据中的规律，导致在训练数据和新数据上都表现不佳。欠拟合的模型没能学习到足够多的特征，通常是因为模型太过简单，或者训练不充分。例子：欠拟合可以类比为一个学生只复习了一些基础知识，但没有足够深入地理解课程内容，结果不仅在模拟考试中表现差，在实际考试中也是如此。

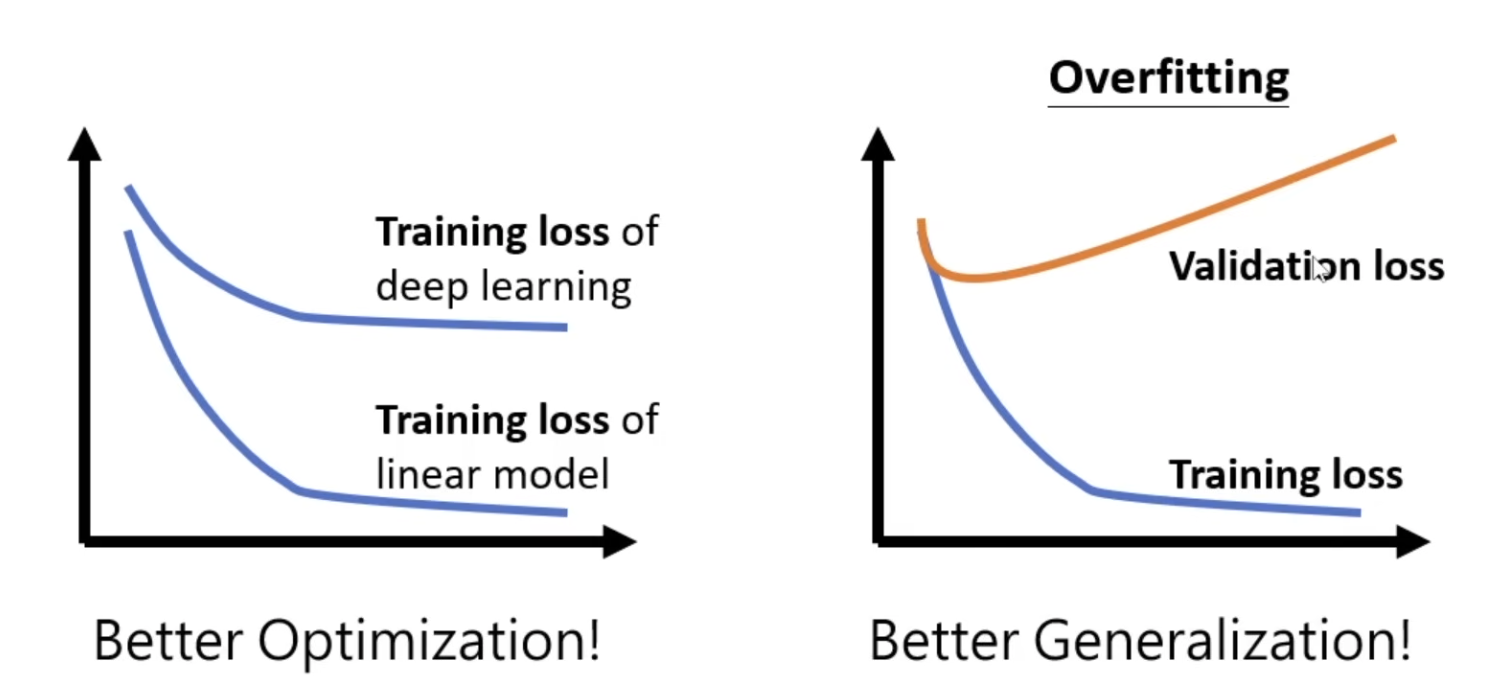
识别需要更好的 Optimization 还是更好 Generalization 。如果深度模型比线性模型得到的 loss 高，需要一个更好的 Optimization。如果 Learning rate 降的已经足够低了但 loss 就是降不下去，是 Overfitting，则需要更换一个更好的泛化方程（Generalization）

image.png|550

文章学习自：李宏毅课程