计算
计算
一、优化运筹
某企业拟生产甲、乙、丙、丁四个产品。每个产品必须依次由设计部门、制造部门和检验部门进行设计、制造和检验,每个部门生产产品的顺序是相同的。各产品各工序所需的时间如下表所示:
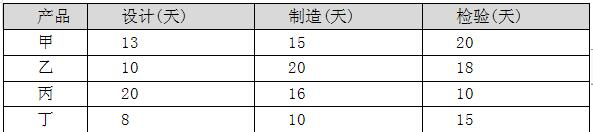
只要适当安排好产品生产顺序,企业最快可以在( )天全部完成这四个产品。
- A、84
- B、86
- C、91
- D、93
本题考查数学应用的能力(优化运筹)。
节省时间的安排方法必然是紧随衔接和尽可能并行安排生产。
第1个产品的设计和最后1个产品的检验是无法与其他工作并行进行的,因此,==应安排“首个设计时间+末个检验时间”尽可能短。为此,应先安排生产丁,最后安排生产丙==。
如果按丁、甲、乙、丙顺序实施,则共需84天,如下图所示。
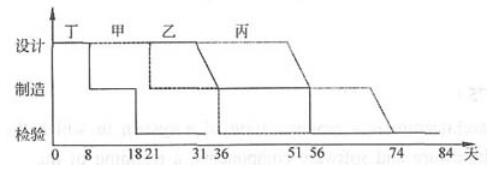
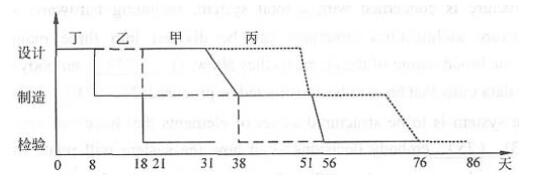
如果按丁、乙、甲、丙顺序实施,则共需86天,如下图所示。
二、计算概率
1路和2路公交车都将在10分钟内均匀随机地到达同一车站,则它们相隔4分钟内到达该站的概率为( )。
- A、0.36
- B、0.48
- C、0.64
- D、0.76
正确答案: C
【答案解析】
本题考查数学应用能力(概率)。
设1路和2路公交车将分别在x和y分钟内到达该站,则x和y是在[0,10]内独立均匀分布的随机变量。本题需要计算||x-y|≤4的概率。
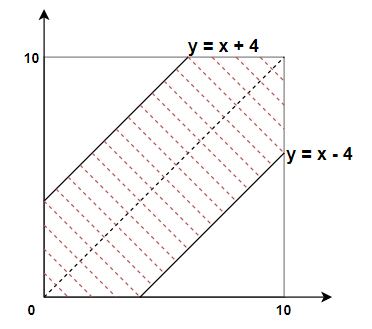
平面上的点(x,y)必然在正方形[0,10;0,10]内均匀分布。|x-y|≤4的概率应当等于该正方形|x-y|≤4的部分面积的比例。
该正方形的面积为100,其中|x-y|≤4部分的面积为64(如下图),因此,|x-y|≤4的概率为0.64。
三、灵敏性分析
实际问题的数学模型往往都是近似的,常带有多个参数,而参数会随环境因素而变化。根据数学模型求出最优解或满意解后,还需要进行==灵敏性分析==,对计算结果进行检验,分析计算结果对参数变化的反应程度。如果对于参数的微小变化引发计算结果的很大变化,那么这种计算结果并不可靠,并不可信。
四、盈利平衡
某厂生产的某种电视机,销售价为每台2500元,去年的总销售量为25000台,固定成本总额为250万元,可变成本总额为4000万元,税率为l6%,则该产品年销售量的盈亏平衡点为 (70)台(只有在年销售量超过它时才能盈利)。
- A、5000
- B、10000
- C、15000
- D、20000
正确答案: A
【答案解析】
1、根据题意计算出每台电视机的可变成本:
4000*10000/25000=1600(元)
2、设盈亏平衡点为X台,则有:
收益=单价*数量*(100%-税率)=2500*X*(100%-16%)
成本=固定成本+可变成本=250*10000+1600*X
收益=成本时,盈亏平衡,因此2500*X*(100%-16%)=250*10000+1600*X
3、解上述方程得,X=5000
五、选择决策
某系统集成项目为满足某种软件产品的市场需求,拟提出自主开发、部分研发任务外包和外购3个方案。假设各方案中销路好的概率为0.3,销路一般的概率为0.5,销路差的概率为0.2。不同销路的损益值如下表所示。假设该项目经营期为10年,那么该项目所作的决策最可能是()。

- A、选择自主开发方案
- B、选择部分研发任务外包方案
- C、选择外购方案
- D、条件不足,无法得出结论
正确答案: A
【答案解析】
自主开发方案的期望值计算方法为:
(80×0.3+60×0.5+50×0.2)×10-300=340(万元)
部分研发任务外包方案的期望值计算方法为:
(30×0.3+20×0.5+15×0.2)×10-80=140(万元)
外购方案的期望值计算方法为(50×0.3+40×0.5+25×0.2)×10-160=240(万元)
由于340>240>140,因此从货币期望值最大决策角度考虑,建议该项目选择自主开发方案。
最小生成树
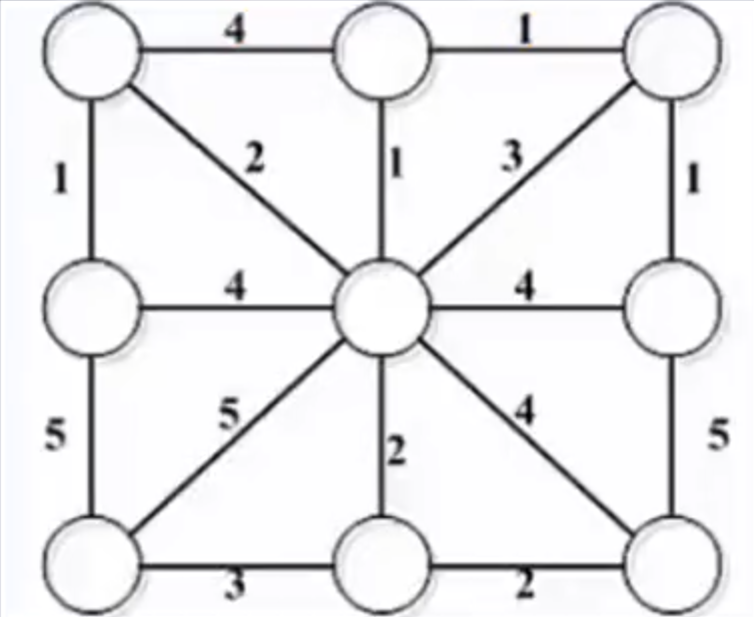
开发商需要在某小区9栋楼房之间铺设自来水管道,使各楼都能连通,又能使总成本最低。经勘查,各楼房之间铺设管道的路径和成本(单位:千元)如图所示,该项目的总成本至少需要()千元。
A. 13
B. 14
C. 15
D. 16